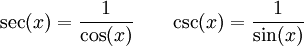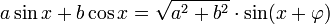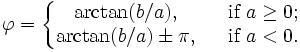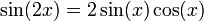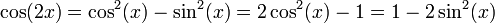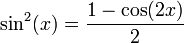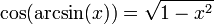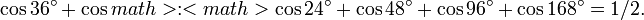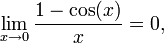삼각함수 항등식들

알고리즘/게임 수학 / 물리

삼각함수 항등식들

중년 플머 김씨 2007. 9. 20. 13:45

삼각함수 항등식(三角函數恒等式)은 삼각함수가 나오는 항등식을 말한다. 이 공식들은 삼각함수가 나오는 복잡한 식을 간단히 정리하는 데 유용하며, 특히 치환적분에서 매우 자주 쓰이기 때문에 중요하다.

참고로 아래에서 $sin 2$ , $cos 2$ 등의 함수는 $sin 2 (x) = (sin(x)) 2$ 와 같이 정의된다.

[편집] 삼각함수의 정의에서

$\cos(x) = \sin\left( x + {\pi \over 2} \right)$

$\tan (x) = \frac {\sin (x)} {\cos(x)} \qquad \operatorname{cot}(x) = \frac {\cos (x)} {\sin(x)} = \frac{1} {\tan(x)}$

$\operatorname{sec}(x) = \frac{1} {\cos(x)} \qquad \operatorname{csc}(x) = \frac{1} {\sin(x)}$

[편집] 주기성, 대칭성, 이동(Shifts)

다음 관계는 단위원을 사용하면 쉽게 보일 수 있다.

다음 식은 삼각함수의 주기성을 나타낸다.

$\sin(x) = \sin(x + 2k\pi) \qquad \cos(x) = \cos(x + 2k\pi) \qquad \tan(x) = \tan(x + k\pi)$

$\sec(x) = \sec(x + 2k\pi) \qquad \csc(x) = \csc(x + 2k\pi) \qquad \cot(x) = \cot(x + k\pi)$

다음 식은 삼각함수의 대칭성을 나타낸다.

$\begin{matrix} \sin(-x) = -\sin(x), & & \sin\left({\pi \over 2} - x\right) = \cos(x), & & \sin\left(\pi - x\right) = \;\;\sin(x) \\ \cos(-x) =\;\;\cos(x), & & \cos\left({\pi \over 2} - x\right) = \sin(x), & & \cos\left(\pi - x\right) = -\cos(x) \\ \tan(-x) = -\tan(x), & & \tan\left({\pi \over 2} - x\right) = \cot(x), & & \tan\left(\pi - x\right) = -\tan(x) \\ \cot(-x) = -\cot(x), & & \cot\left({\pi \over 2} - x\right) = \tan(x), & & \cot\left(\pi - x\right) = -\cot(x) \\ \sec(-x) =\;\;\sec(x), & & \sec\left({\pi \over 2} - x\right) = \csc(x), & & \sec\left(\pi - x\right) = -\sec(x) \\ \csc(-x) = -\csc(x), & & \csc\left({\pi \over 2} - x\right) = \sec(x), & & \csc\left(\pi - x\right) = \;\;\csc(x) \end{matrix}$

다음은 삼각함수의 이동 성질을 나타낸다.

$\begin{matrix} \sin\left(x + {\pi \over 2}\right) = \;\;\cos(x), & & \sin\left(x + \pi\right) = - \sin(x) \\ \cos\left(x + {\pi \over 2}\right) = - \sin(x), & & \cos\left(x + \pi\right) = - \cos(x) \\ \tan\left(x + {\pi \over 2}\right) = - \cot(x), & & \tan\left(x + \pi\right) = \;\;\tan(x) \\ \cot\left(x + {\pi \over 2}\right) = - \tan(x), & & \cot\left(x + \pi\right) = \;\;\cot(x) \\ \sec\left(x + {\pi \over 2}\right) = - \csc(x), & & \sec\left(x + \pi\right) = - \sec(x) \\ \csc\left(x + {\pi \over 2}\right) = \;\;\sec(x), & & \csc\left(x + \pi\right) = - \csc(x) \end{matrix}$

또한, 주기가 같지만, 상(phase)이 다른 사인파들의 선형결합은 또 다른 상의 동일주기의 사인파가 된다. 즉, 다음과 같다.

$a\sin x+b\cos x=\sqrt{a^2+b^2}\cdot\sin(x+\varphi)$

여기서

$\varphi= \left\{ \begin{matrix} {\rm arctan}(b/a),&&\mbox{if }a\ge0; \; \\ {\rm arctan}(b/a) \pm \pi,&&\mbox{if }a<0. \; \end{matrix} \right. \;$

[편집] 피타고라스 정리

$\sin^2(x) + \cos^2(x) = 1 \qquad \tan^2(x) + 1 = \sec^2(x) \qquad \cot^2(x) + 1 = \csc^2(x)$

[편집] 덧셈 정리

다음을 증명하는 가장 쉬운 방법은 오일러의 공식을 이용하는 것이다. 탄젠트 공식은 위의 둘을 결합하여 얻는다.

$\sin(x \pm y) = \sin(x) \cos(y) \pm \cos(x) \sin(y)\,$

$\cos(x \pm y) = \cos(x) \cos(y) \mp \sin(x) \sin(y)\,$

(좌변에 "+" 기호가 있는 경우, 우변에는 "−" 기호를 사용함.)

$\tan(x \pm y) = \frac{\tan(x) \pm \tan(y)}{1 \mp \tan(x)\tan(y)}$

${\rm c\dot{\imath} s}(x+y)={\rm c\dot{\imath} s}(x)\,{\rm c\dot{\imath} s}(y)$

${\rm c\dot{\imath} s}(x-y)={{\rm c\dot{\imath} s}(x)\over{\rm c\dot{\imath} s}(y)}$

여기서

${\rm c\dot{\imath} s}(x) = \exp(i x) = e^{i x} = \cos(x)+i \sin(x)\,$

$i^{2}=-1.\,$

[편집] 두배각 공식

다음 공식은 바로 위 덧셈 공식에서 $x = y$ 로 놓으면 바로 얻어진다. 피타고라스의 식을 쓰면 변형을 얻는다. 또한 드 무아브르의 공식(de Moivre's formula)에서 $n = 2$ 로 놓아도 된다.

$\sin(2x) = 2\sin(x)\cos(x) \,$

$\cos(2x) = \cos^2(x) - \sin^2(x) = 2 \cos^2(x) - 1 = 1 - 2 \sin^2(x) \,$

$\tan(2x) = \frac{2 \tan (x)} {1 - \tan^2(x)}$

$\frac{\tan^2(x)-1}{\tan(x)} = -2 \tan(2x)$

[편집] n배각 공식

T_n이 n번째 체비셰프 다항식(Chebyshev polynomial)일 때,

cos(n x) = T n (cos(x))

드 무아브르의 공식(De Moivre's formula):

cos(n x) + i sin(n x) = (cos(x) + i sin(x)) n

The Dirichlet kernel D_n(x) is the function occuring on both sides of the next identity:

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots+2\cos(nx)=\frac{\sin\left(\left(n+\frac{1}{2}\right)x\right)}{\sin(x/2)}$

The convolution of any square-integrable function of period 2π with the Dirichlet kernel coincides with the function's nth-degree Fourier approximation.

[편집] 차수 줄이기

두배각 공식의 코사인 공식을 cos²(x) 과 sin²(x)으로 푼다.

$\cos^2(x) = {1 + \cos(2x) \over 2}$

$\sin^2(x) = {1 - \cos(2x) \over 2}$

[편집] 반각 공식

차수 줄이기 공식의 x/2 를 x 로 바꾸어 넣고, cos(x/2) 과 sin(x/2)으로 푼다.

$\left|\cos\left(\frac{x}{2}\right)\right| = \sqrt{\left(\frac{1 + \cos(x)}{2}\right)}$

$\left|\sin\left(\frac{x}{2}\right)\right| = \sqrt{\left(\frac{1 - \cos(x)}{2}\right)}$

tan(x/2)는 sin(x/2) / cos(x/2)과 같고, 여기에 분자 분모에 같은 2cos(x/2)을 곱한다. 그러면, 분자는 사인의 두배각 공식에 의해 sin(x)이 되고, 분모는 2cos²(x/2) - 1 + 1 이므로 코사인 두배각 공식을 쓰면 cos(x) + 1 이 된다. 두번째 식은 분자와 분모에 다시 sin(x)를 곱하고, 피타고라스 공식으로 간단히 하면 얻어진다.

$\tan\left(\frac{x}{2}\right) = \frac{\sin(x)}{\cos(x) + 1} = \frac{1 - \cos(x)}{\sin(x)}$

[편집] 곱을 더하기로

우변을 덧셈정리로 전개하면 증명된다.

$\cos(x) \cos(y) = {\cos(x + y) + \cos(x - y) \over 2}$

$\sin(x) \sin(y) = {\cos(x - y) - \cos(x + y) \over 2}$

$\sin(x) \cos(y) = {\sin(x + y) + \sin(x - y) \over 2}$

[편집] 더하기를 곱으로

위 식의 x를 (x + y) / 2 로, y 를 (x - y) / 2 로 바꾼다.

$\sin(x) + \sin(y) = 2 \sin\left( \frac{x + y}{2} \right) \cos\left( \frac{x - y}{2} \right)$

$\cos(x) + \cos(y) = 2 \cos\left( \frac{x + y}{2} \right) \cos\left( \frac{x - y}{2} \right)$

[편집] 삼각함수의 역함수

x > 0 이면

$\arctan(x)+\arctan(1/x)=\frac{\pi}{2}.$

만약 x < 0 이면, 등식 우변이 -π/2가 된다.

$\arctan(x)+\arctan(y)=\arctan\left(\frac{x+y}{1-xy}\right)$

피타고라스 정리로 부터 다음과 같은 몇가지 항등식을 얻는다.

$\cos(\arcsin(x))=\sqrt{1-x^2}$

== 변수 없는 항등식 == ---- ---- ---- ---- 여기에 위키 문법을 사용하지 않을 글을 적어 주세요

리처드 파인만은 소년 시절에 다음의 기묘한 식을 배우고 언제나 기억했다고 알려져 있다.

$\cos 20^\circ\cdot\cos 40^\circ\cdot\cos 80^\circ=1/8.$

그러나, 이 식은 다음의 변수를 포함한 일반적인 식의 특수한 경우이다. (x=20˚, k=3을 넣고, sin x = sin (180˚-x)를 이용 우변정리.)

$\prod_{j=0}^{k-1}\cos(2^j x)=\frac{\sin(2^k x)}{2^k\sin(x)}.$

다음 식들은 아마 변수가 있는 일반화된 식을 찾기가 위 보다 어려울 것이다.

$\cos 36^\circ+\cos math> :<math>\cos 24^\circ+\cos 48^\circ+\cos 96^\circ+\cos 168^\circ=1/2.$

21을 택해서 각을 나누면, 도로 표현한 각이 더이상 깔끔하지 않다. 다음 식을 보자.

$\cos\frac{2\pi}{21}+\cos\frac{2(2\pi)}{21}+\cos\frac{4(2\pi)}{21}+\cos\frac{5(2\pi)}{21}+\cos\frac{8(2\pi)}{21}+\cos\frac{10(2\pi)}{21}=1/2.$

1, 2, 4, 5, 8, 10 이란 인자를 보면 차츰 답이 드러난다. 이 수들은 모두 21/2보다 작고, 21과의 공약수가 1인 수 들이다. 사실, 위 세가지 예는 더 인수분해되지 않는 원분다항식(cyclotomic polynomial)에 대한 기본정리의 따름정리이다. 코사인값은 다항식의 영(zero)들의 실수부이고, 그들의 합은 21(가장 마지막 예)의 뫼비우스 함수값이다. (식에선 값의 반만이 나타난다.)

[편집] 미적분학

미적분학의 삼각함수에선 각을 라디안(radian)으로 써야 한다. 그렇지 않으면, 다음 관계식들은 성립하지 않는다. 우선 삼각함수가 기하학적으로 정의된 후에 함수들의 미분을 구하기 위해선 우선:

$\lim_{x\rightarrow 0}\frac{\sin(x)}{x}=1,$

과

$\lim_{x\rightarrow 0}\frac{1-\cos(x)}{x}=0,$

을 증명한다. 그리고, 미분의 극한 정의와 덧셈정리를 이용한다. 삼각함수가 테일러 급수로 정의되었다면, 각 항을 미분하여 알아낼 수 있다.

${d \over dx}\sin(x) = \cos(x)$

나머지 삼각함수의 미분은 위 항등식과 미분법칙으로 얻어진다.

적분식은 적분표를 참고하라.

원본 주소 ‘http://ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98_%ED%95%AD%EB%93%B1%EC%8B%9D’

티스토리